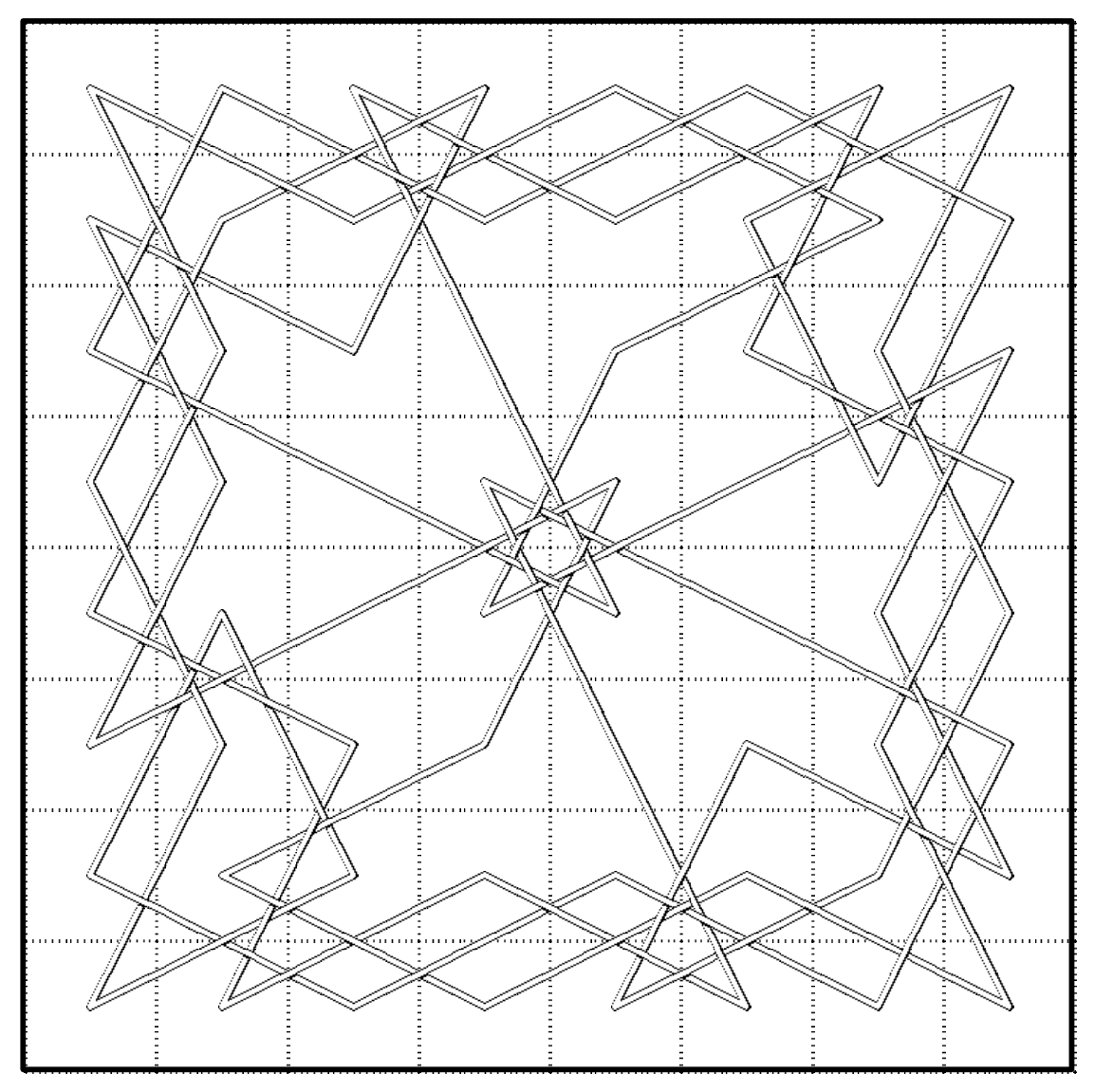
In 1997 Brendan D. McKay proved (without actually constructing them) that the total number of closed knight’s tours on a 8X8 board is exactly 13,267,364,410,532.

Don Knuth pondered the possibility of constructing the tours:

"Thirteen trillion is indeed a huge number. Yet it isn’t completely out of reach. If we can visit one tour every microsecond, we can visit them all in 13 million seconds, which is about 5 months. Also, if we represent each tour as a 168-bit vector that shows which edges are used, we can store all the tours in about 279 terabytes."

Last night I found the number of closed knight's tours on a 9X9 board! In order not to steal anyone's priority, I will give priority to whoever posts the answer to this message within the next 24 hours.

In the meantime, the rest of us can look at this nice example of a tour that Knuth showed in his Christmas lecture.